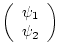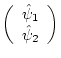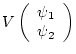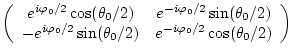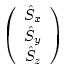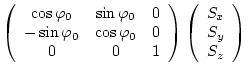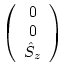



Next: 2.15 TSPNROTの機能
Up: 2 計算制御パラメータ
Previous: 2.13 TACCELEの機能
2.14 TSPNSETの機能
NSPIN=4のときに有効なフラグである。
システム全体の絶対的なスピン方向を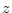 軸
などにそろえるときに用いる。
軸
などにそろえるときに用いる。NBEG=0,1のときに、
MDが始まる前に1回だけ波動関数を変換する。
KROT=1および2が有効である。
KROT=2とKROT=1を連続して用いたい場合
でも2回のジョブに分けて行わなければならないようになっている。
ver25からは、KROT=3も使用可能となっている。このフラグが
立ったときには、NBEG=0,1で波動関数を読みに行った後、
ファイルspnrot.datが読まれて、波動関数を変換する。
ファイルは、sample.dat.shに書くようになっており、
下記のように入力する。ただし、読み込まれるのは、1行目だけである。
KROT=3の場合は、回転の仕方を制限して2回の回転を連続的に行なう。
1回目の回転でシステム全体の絶対的なスピン方向を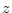 軸にそろえ(
軸にそろえ(SX,SY,SZ
に回転前の磁気モーメントを指定する)、2回目の回転でSXX,SYY,SZZで指定した
磁気モーメントのy成分が消えるように回転させる。
cat > ${tmpdir}/spnrot.dat << end
2 -5.660817 2.830552 -0.039051 0.0 0.0 1.0 KROT SX SY SZ SXX SYY SZZ
1 1.0 0.0 0.0 0.0 1.0 0.0 KROT SX SY SZ SXX SYY SZZ
3 -5.66 2.83 -0.03 -1.66 0.83 -0.01 KROT SX SY SZ SXX SYY SZZ
end
KROT=2の場合、全系の磁気モーメントを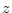 軸方向にするために用いられる。
(SX SY SZ)には、変換前の全系の磁気モーメントを指定し、
軸方向にするために用いられる。
(SX SY SZ)には、変換前の全系の磁気モーメントを指定し、(SXX SYY SZZ)に
(0.0 0.0 1.0)すれば、変換後全系の磁気モーメントは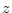 軸方向に向いて
出力される。
この操作によりxおよびy方向の全磁気モーメントがゼロとなる。コリニアー磁気構造
の場合には、各原子の磁気モーメントのxおよびy成分もゼロとなっているはずである。
軸方向に向いて
出力される。
この操作によりxおよびy方向の全磁気モーメントがゼロとなる。コリニアー磁気構造
の場合には、各原子の磁気モーメントのxおよびy成分もゼロとなっているはずである。
KROT=1は、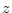 軸回りの回転変換を行うときに使う。
ノンコリニアー磁気構造の場合には、
軸回りの回転変換を行うときに使う。
ノンコリニアー磁気構造の場合には、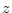 軸方向のモーメントを変化させずに、
軸方向のモーメントを変化させずに、
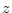 軸回りの回転を行い面内のモーメントの方向を軸方向にそろえておくと便利で
ある。
軸回りの回転を行い面内のモーメントの方向を軸方向にそろえておくと便利で
ある。(SX SY SZ)には、方向をそろえたい原子のモーメントを指定する。
KROT=2の場合の原子の磁気モーメントの出力結果を指定すればよい。
そのとき(SXX SYY SZZ)には、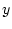 軸方向にそろえたいたいときは、
軸方向にそろえたいたいときは、
(0.0 1.0 1.0)としてすればよい。
実際には、上記の操作は、波動関数の位相を変換して行っている。
その操作の定義は、以下の様である。
変換前の波動関数と変換後のものをそれぞれ、
とすると変換は、
である。
KROT=1の場合は、磁気モーメントベクトルに対して
の関係式より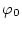 を求める。ここで
を求める。ここで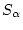 は、変換前の
磁気モーメントベクトル、
は、変換前の
磁気モーメントベクトル、
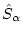 は変換後の磁気モーメントベクトル
であり、
は変換後の磁気モーメントベクトル
であり、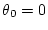 を仮定している。
を仮定している。KROT=2の場合は、
磁気モーメントベクトルに対して
の関係式より
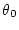 と
と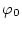 を求める。
を求める。




Next: 2.15 TSPNROTの機能
Up: 2 計算制御パラメータ
Previous: 2.13 TACCELEの機能
Copyright (C), Tatsuki Oda (oda@cphys.s.kanazawa-u.ac.jp, Kanazawa University)