3.1 格子(セル)定数の入力

Next: 3.1.1 IBRAV=1 単純立方格子 Up: 3 計算対象パラメータ Previous: 3 計算対象パラメータ

3.1 格子(セル)定数の入力

1 20.0 0.0 0.0 0.0 0.0 0.0 6.0 0 IBRAV,(CELLDM(I),I=1,6),RLATMX,JRLTSM

IBRAVは、14種類のブラベ格子を指定する。この計算コードでは、各格子の基本並進ベクトルを直交基底ベクトル $({\bf x},{\bf y},{\bf z})$ に対する表現ベクトルとして確保している。表現ベクトルにはいろいろな採り方が存在し、同じブラベ格子でも 2つ以上の表現ベクトルが用意されている場合がある。過去に定義されたものを残しているだけの場合もある。 (数学的には、不必要かもしれないが、行列式が正になるように基本並進ベクトルの順番を並べている。) IBRAVの値の下2桁がブラベ格子の番号を表し、 3桁以上は、表現ベクトルの区別に使用している。

一般的に単位胞の基本並進ベクトルを $({\bf a}_{1},{\bf a}_{2},{\bf a}_{3})$ とすると、逆格子空間の基本並進ベクトルは、

$\displaystyle ({\bf b}_{1},{\bf b}_{2},{\bf b}_{3})$

$\textstyle =$

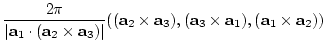$\displaystyle \frac{2 \pi}{ \vert {\bf a}_{1} \cdot ({\bf a}_{2} \times {\bf a}... ...\bf a}_{3}),({\bf a}_{3} \times {\bf a}_{1}), ({\bf a}_{1} \times {\bf a}_{2}))$

(18)

によって計算されており(分母は、絶対値になっている)、直交基底 $\frac{2\pi}{a}({\bf x},{\bf y},{\bf z})$ の表現ベクトルで計算コード中に確保している。

基本的には、CELLDM(I)(I=1-6)から6個の格子定数(長さは、a.u.単位)を定めている。 CELLDM(I)の指定の仕方は、IBRAVの値によって必要最小限の決まった量を指定するようになっている。上記の例では、IBRAV=1で立方体のセルの指定となっている。このときは、セルの1辺の長さをCELLDM(1)に指定して、それ以外のCELLDM(I)は、ゼロとしておく。(ソースコードのlatgen.fを参照。)

Subsections

Next: 3.1.1 IBRAV=1 単純立方格子 Up: 3 計算対象パラメータ Previous: 3 計算対象パラメータ