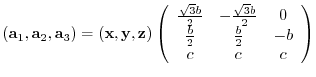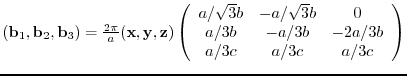



Next: 3.1.8 IBRAV=105 simple trigonal
Up: 3.1 Input of lattice
Previous: 3.1.6 IBRAV=4 simple hexagonal
3.1.7 IBRAV=5 simple trigonal lattice(�$BC1=c;0J}3J;R�(B)
CELLDM(1) 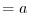 ,
CELLDM(4)
,
CELLDM(4)
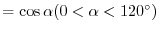 ,
,
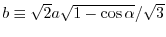 ,
,
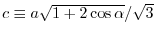
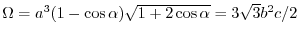
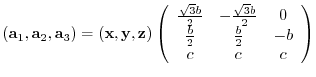
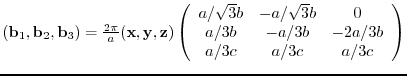
Relationship with a lattice constant of hexagonal lattice and choice of the sub-lattice.
�$BO;J}3J;R3J;RDj?t$H$N4X78$*$h$SI{3J;R$N$H$jJ}�(B
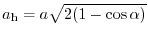 ,
,
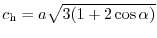
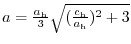 ,
,
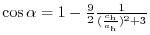
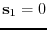
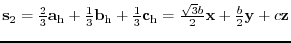
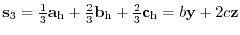




Next: 3.1.8 IBRAV=105 simple trigonal
Up: 3.1 Input of lattice
Previous: 3.1.6 IBRAV=4 simple hexagonal
Copyright (C), Tatsuki Oda (oda@cphys.s.kanazawa-u.ac.jp, Kanazawa University)