【ラシュバ効果】
1960年にE. Rashbaによって提唱された効果。界面や表面などの系は、面の法泉に垂直な方向に２次元系を形成している。この２次元電子系において、面直方向（面に垂直な方向）に電位差を与えることによって非磁性体であってもスピン偏極電子が生じ、電子スピンについて縮退していた電子状態にスピン分裂が現れる現象で、分裂した電子バンドが観測される（図１）。電子の波数ベクトルは表面平行方向であり、スピン偏極ベクトルは二次元面内のみを向いている。面直方向の対称性が破れていることによってその方向に電位差が生じ、スピン偏極電子が生じる。
この効果においては、表面での「空間反転対称性の破れ」と「表面電場の効果」が重要となる。界面においてもこの効果は観測されており、スピン偏極ベクトルの方向が２次元面内に制約する効果をもつ。この効果は、電子が光の速度に近い高速で運動することにより現れる相対論効果の一つであり、スピン軌道相互作用を起源とするものである。これまでマクロな現象においては大きな関心を集めていなかったが、近年、電子デバイスなどの微細化が動機付けとなり、微細加工技術の進歩および観測実験技術の進歩とが相まって、このような効果を積極的に解明し、電子デバイスに応用する必要性が求められている。スピン軌道相互作用は小さなエネルギースケールであり、このような効果を積極的に活用することにより電子デバイスにおける低エネルギー消費・高速化・コンパクト化・高効率化を目指している。基礎科学としても、表面・界面におけるスピン軌道相互作用の解明が十分に進んでいないのが現状である。次世代エレクトロニクスであるスピンエレクトロニクスでは、電子に働くスピン軌道相互作用を解明し、十分に活用することがその中心的課題である。
この効果を説明する理論は比較的分かり易いと思われるので以下に説明する。理系大学生の３年生以上程度の説明を目指したつもりである。２次元面内へ閉じ込められた自由電子が、スピン軌道相互作用を受ける系を考える。ハミルトニアンは、
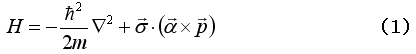
のように書くことができる。自由電子の運動エネルギーとスピン軌道相互作用との和である。ここで、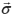
および
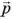は電子のスピン演算子（パウリ行列の演算子）および運動量演算子である。また、
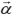は面直方向の相互作用ベクトルを表し、有効な電場ベクトルと解釈することができる。
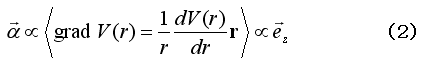
電子が自由電子であるとき、次のように波動関数が与えられる。
このとき運動量は、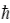
と波数ベクトル
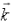との積で与えられて、
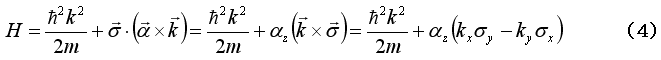
と書くことができる。スピン軌道相互作用の部分（式（４）の第２項）は、波数ベクトル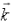にも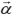にも垂直なスピン方向のときに相互作用が存在するようになっている。解くべき方程式は、
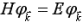である。固有値は、
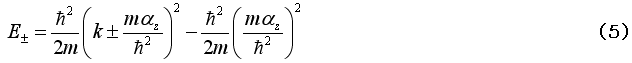
で与えられ、それぞれの固有値に属する固有ベクトルは、
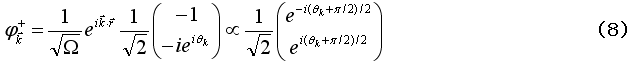
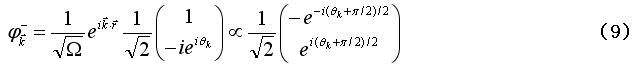
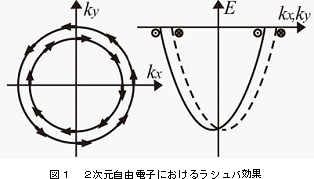
である。式（５）からは、波数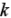
の２次関数で与えられる自由電子の固有値が、スピン偏極の方向によりエネルギーの変更を受けることが分かる。その様子は、図１に示されている。
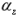はラシュバパラメータと呼ばれラシュバ効果の大きさを示す量である。図１の場合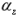は正に採られていることになる。式（８）および（９）の固有ベクトルでのスピン演算子の期待値は、
である。この式からも分かるように、電子スピンの偏極方向は
面内であり、図１に示すように波数空間上の原点を中心とした円の接線方向を向いている。電子バンドの構造は、波数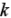について下に凸の２次関数的なものだけではなく、上に凸の構造の場合も存在する。この場合は、有効質量である
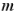が負になっていると考えればよい。電子スピンは角運動量であり、時間反転に対して角運量ベクトルの方向が逆向きになる。また波数ベクトルについても同様である。式（１０）と式（１１）では時間反転について、
というような関係が成立していること（（１０）式と（１１）式の右辺で
に
を代入すると式が入れ替わる）が分かる。つまり時間反転対称性は保持されている。一方、空間反転については、
であるので、空間反転対称性は破れていることになる。
ラシュバパラメータは、面直方向のポテンシャル勾配の大きさを表しているが、表面や界面が固有にもっている勾配だけでなく、外部電場により作りだされる勾配により、ラシュバ効果の大きさを調整することが可能である。例えば、電界効果トランジスタのゲート電圧を変化させることによりラシュバ効果を制御し、間接的に電子のスピン偏極や磁性特性を制御するようなスピントロニクスを考えることができるであろう。