【スピン軌道相互作用】
電子は質量、電荷の他に, スピン角運動量という粒子固有な物理量を持っている。スピン角運動量は磁場に応答する磁気モーメントの起源であり、電子は磁場中で２つの異なったエネルギー状態に分離している。一方、電荷をもつ電子が、軌道運動することにより、この軌道電流が磁場を生み出す。したがって、電子のスピン磁気モーメントは、軌道電流の生み出す磁場と互いに相互作用（力）をおよぼし合う。軌道電流は電子の軌道角運動量に置き換えて述べることができて、この相互作用は、スピン軌道相互作用と呼ばれている。この相互作用は、常に存在しているが、もともと電磁気作用中でも磁気的作用を媒介にしているため、電気的な作用よりも極端に小さなエネルギーにより支配されている。そのため普段はあまり意識することがないかもしれない。しかしながらこのエネルギーの小いささは、将来の低エネルギー消費化社会実現のために欠かせないものである。
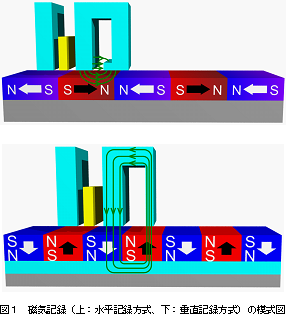
このスピン軌道相互作用に支配されている現象として、最も日常的なものは磁石である。磁石は強力な電磁石から、コンピュータのデータ記憶装置に使われている磁気記録媒体まで非常に幅広く、しかも記憶媒体などを例にとればすぐに想像できるように記憶するためにエネルギーをほとんど消費しない。より平易な言葉で言い換えれば、永久磁石と呼ばれる磁石は長期間その磁石の性質を失わず、N極とS極の情報を記憶している。その記憶（メモリ）を書き換えるときにエネルギーを必要としているだけである。蛇足かもしれないがコンデンサーなどの電気を使った記憶には電気をためておくために極板間の電位を保ちつづけなければならない。話をもとに戻すと、つまり、スピン軌道相互作用を使った現象を使うことにより格段に、エネルギー消費を抑えることが可能となると考えられている。
現在、情報化社会を支える電子機器内では、電子の電荷を移動させることにより情報を伝達し、目的の機能を達成しており、このような技術を一般に、エレクトロニクス技術と呼んでいる。電荷の移動には電子の散乱、つまり、ジュール熱の発生を伴うため、帰還させることができない大量のエネルギーを消費してしまっている。このために移動する距離を小さくし、散乱機会を減らす努力つまりデバイスの小型化も推進されている。さらなる小型化には、電子の量子効果をよくよく考えて電子機器の機能を向上させる努力が続けられている。量子効果を考えだすと、電子のもっている情報は、電荷だけでなくスピンの情報もある。電子スピンの情報は、N極とS極に相当する情報量つまり、２倍の情報を持つことが可能となる。電子の移動により以前よりも２倍の情報を伝達することができる可能性がある。このように電子スピンの自由度も取り入れる電子デバイスの技術をスピンエレクトロニクス(スピントロニクスという造語も使われる)と呼んでいる。スピントロニクス技術の重要な視点は、この技術がエレクトロニクス技術の基盤の上に構築されようとしているため、電気的制御法により、スピンのような磁気的な情報を操作したり伝達したりする必要が生じていることである。要は、スピン軌道相互作用の物質中での基礎研究が非常に重要となっているのである。
スピン軌道相互作用は、白金、金、あるいは、鉛といった重い元素で顕著に現れる。また磁性体での磁気異方性の起源としてスピン軌道相互作用が重要となる。電子は原子核の周りを軌道運動している。古典電磁気学により、スピン軌道相互作用を考えると、電子のスピン角運動量と軌道角運動量との相互作用という形で書くことができる。
ここで、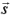
はスピン角運動量、
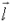は軌道角運動量であり、
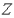は原子の原子番号、そのほかそれぞれ
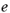:電子の電荷、
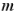:電子の質量、
:光の真空中での速度、
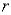:電子の原子核からの距離である。
スピン軌道相互作用は、相対論的量子力学により自然に導かれる。原子核の電荷は、原子番号Zに比例して大きくなる。この電荷と電子の電荷は大きなクーロン相互作用により引き合っている。電子が原子核に近づくときには、非常に大きな速度をもつと考えられる。価電子が水素原子の平均的な半径（ボーア半径）の100分の１の距離まで原子核に近づいたときに、その速度を古典的な考え方で見積もると、鉛原子の場合には、光速の３分の１程度の速さになる。そこで、通常の量子力学を拡張した相対論的量子力学にて、スピン軌道相互作用を考えなければならない。つまりシュレディンガー方程式の代わりにディラック方程式を考えることになる。ディラック方程式は、シュレディンガー方程式に比べてその構造が複雑である。ディラック方程式を直接考えるよりも、シュレディンガー方程式に付加的なスピン軌道相互作用を加えた拡張を行って、通常の量子力学にスピン軌道相互作用を加えただけでも十分な場合が多々あるので、通常の量子力学の知識を使って考えることもできる。スピン軌道相互作用を加えたハミルトニアンは、
と書くことができる。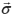
および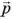
は電子のスピン演算子（パウリ行列の演算子）および運動量演算子である。右辺第２項目がスピン軌道相互作用をあらわす演算子である。
は相対論効果を考えないときのポテンシャルで、主に電子に作用する原子核からのクーロン相互作用を含んでいる。を原子核からのクーロン相互作用に限定すると、
となり、
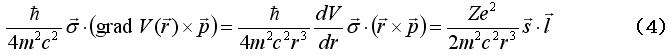
と書くことができる。この式は因子２を除いて式（１）と同じである。この因子２は相対論効果から来るものである。