【高校生・大学生への解説】
物質科学の研究は、これまで固体を対象としてきた。固体の結晶は、原子が規則的に３次元的に配列している。これを並進対称性と呼んでいる。この対称性のために単純で数学上の取り扱いも、解析的に進めることができる。もちろんこのような結晶にも十分おもしろい科学があるのだが、物質の本当の面白い姿は、規則的でない乱れた姿の中にある。最近の最先端の技術は、一様ではなく、結晶ではない物質の性質が利用されるようになり、表面あるいは界面といった場所は、その典型的な例である。
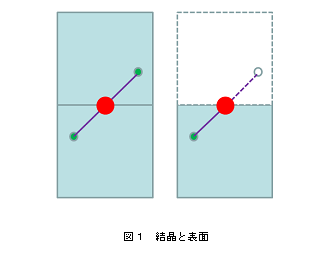
ここでは、３次元結晶からすこし規則性がなくなった「表面」を考えよう。規則的に原子が配列した結晶をある面で切断すると２つの表面が出来上がる。これの片方を表面と呼ぶ。荒っぽいことを言えば、身の回りのものは、すべて表面が我々の目に映っている。この表面では、結晶の片側がなくなったのであるから、なくなった原子配列に関する規則性がなくなってしまっている。表面に立てた法線方向を通常、「面直方向」、それに垂直な方向を「面内方向」と呼んでいる。前者の面直方向には、結晶では存在していた対称性のうちで、並進対称性がなくなっている。物理学で、存在していた対称性がなくなることをしばしば、「対称性が破れる」と呼んでいる。表面ができると、もともと空間反転（点対称）の対称性があったものがなくなってしまう。（図１）つまり、空間反転対称の破れが生じるわけである。
図1で別のことを考えよう。赤色の球を原子と考える。この原子は原子核と電子から構成されている。もちろん今考えている物質はすべてそのようなものと考えている。赤い原子の近くにいる電子になってみると、結晶であったときは、空間の上側と下側に原子核も電子も存在して、両方からクーロン相互作用を受けていたが、表面ができて上側がなくなると下側からしかクーロン相互作用を受けなくなり表面の電子にとっては、表面にいる原子核からのクーロン力を強く受けることになる。結果的に表面の平均として、面直方向へ電場が印加した（かかった）のとおなじような効果が現れる。つまり、表面の電子は表面の面直方向へ電場がかかる。
さらに電子のスピンについて触れなければならない。電子は質量、電荷の他に、スピン角運動量という固有の物理量をもっている。地球が地軸の周りに自転していように、電子も自転していると考えると分かりやすい。電子には、右回りと左回りの自転の２つの状態が存在する。別の言い方では、１つの電子につき、２つの状態しか存在しない。ただし、地軸に相当する方向をスピン軸と呼ぶことにすると、そのスピン軸の方向は決まっているわけではなく、その電子以外からの力によって地軸の方向が決まる。
表面での「空間反転対称性の破れ」と「表面電場の効果」により、電子スピンについて面白いことが起こる。この効果は、ラシュバ効果と呼ばれている。表面の面内方向（表面に並行な方向）については、電子の軌道状態を波数ベクトルにて区別することができる。波数ベクトルは、１つの電子の運動量を表しており、電子の速度のようなものと思ってもらってもよい。ラシュバ効果とは、電子のスピン軸が波数ベクトルの方向に垂直でしかも表面に平行に向いており、同じ波数ベクトルをもつ電子を比較すると、スピンが向く方向によりその電子のエネルギーが異なっているのである。このような電子の状態を観測する方法の１つが、光電効果を用いた角度分解光電子分光と呼ばれる測定実験である。まだ実験分解能は落ちるが、スピンまで特定して観測することができるスピン分解の角度光電子分光も行われている。
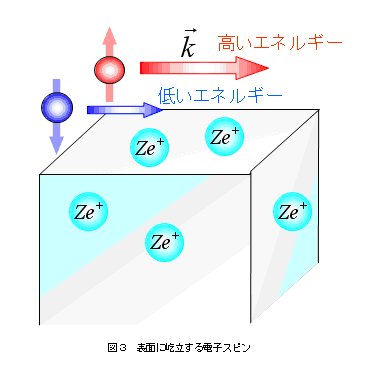
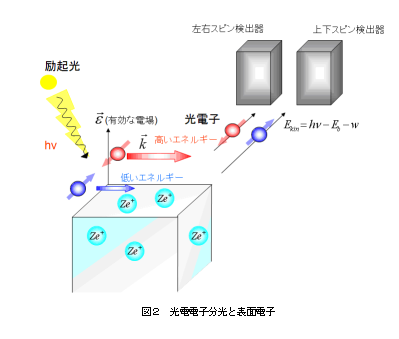
ラシュバ効果による電子の状態を調べる様子を模式的に図２に書いている。光電子分光では、励起光を入射して、放出されてくる電子の運動エネルギーを測定することにより、出てきた電子が表面上でもっていたエネルギーを解析するものである。運動量は放射される電子の方向（放射角）を用いて決定される。電子のスピンについては、検出器の配置を考慮して左右方向のスピン軸を検出する場合と上下方向を検出する場合などがある。表面内の１つの電子のエネルギーが高い場合は、放出される電子の運動エネルギーは大きい。これまでの実験観測では、通常のラシュバ効果にて理解できるように左右方向のスピンを検出する検出器にて、表面内での電子エネルギーの分離（高いエネルギーと低いエネルギー）が観測されていた。今回の実験観測では、上下方向の検出器にてエネルギー分離を起こしている電子の状態を発見した。つまりある特定の波数ベクトルをもつ電子で、スピン軸が表面に垂直なものを発見したのである。（図３参照）これは通常のラシュバ効果に従わない電子の発見です。
この発見には、密度汎関数法を用いた第一原理計算が重要な役割を担っていました。電子は量子力学に従う粒子ですので、
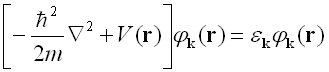
のような方程式を解くことより電子の運動が得られます。[ ]内はハミルトニアンと呼ばれ、電子の運動エネルギーとポテンシャルエネルギーの和で表せます。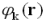
および
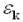は状態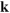
で指定される波動関数および固有値です。これまで、電子の運動を解く場合には、原子核があまり重い元素ではないと近似して（つまり非相対論的電子として）解いていたのですが、表面にある原子核が重い場合、その電子を相対論的電子として扱う必要があります。今回相対論効果を十分に取り入れた計算プログラムを構築することにより、ラシュバ効果を数値計算で検証することができるようになりました。このような元素の場合は、図２の高いエネルギーと低いエネルギーとの差は、100meV程度にも達するものが、光電子分光などの実験測定で観測されていました。今回の成果も、この大きなラシュバ効果を観測するために開始した実験でありましたが、通常のラシュバ効果とは異なった観測結果が得られました。スピンの向きが表面に垂直な電子状態の発見がそれです。今回、高いエネルギーと低いエネルギーの差は最大で230meVに達しています。近年、光電子分光法の分解能が向上したことが、ラシュバ効果の観測を可能としています。
従来の電子工学であるエレクトロニクスは、電子の電荷が運ばれることにより情報伝達が行われます。つまり電流が流れることにより、電子デバイスがその機能を果たすわけです。次世代のエレクトロニクスでは、通常のエレクトロニクスに加えて、電子スピンの自由度を情報伝達の要素に加えて電子工学を構築しようというものです。これはスピンエレクトロニクスと呼ばれ、スピントロニクスという造語も作られています。次世代のエレクトロニクスであるスピントロニクス分野では、先端的な研究が勢力的に行われています。
スピントロニクスの開発により、低消費電力・高速・高効率・多機能な電子デバイスが実現すると期待されています。電子デバイスでは結晶を２次元的に人工的に積層させて作成させることが多く、表面や界面の特性が重要となります。このような環境においては、電子にはラシュバ効果が現れ、電子スピンは２次元面内の方向を向いております。電子が２次元面内の一方向に移動することを考えた場合には、移動する電子の中にはさまざまな電子スピンをもつものが存在し、異なった方向をもつスピン同士で、散乱を受けてスピン分極の情報が、電子移動とともに減衰しやすく、情報伝達の効率が低下すると考えられています。電子が移動する方向を１次元的にすることによりその効率を低下させないことが考えられています。その他に、電子スピンを２次元面に垂直にさせて移動させることも、伝達効率を下げない方法であると考えられています。そこで今回の発見が、役に立つと考えられます。面に垂直な電子スピンが、原子核などに散乱されずに情報を伝達できるわけです。
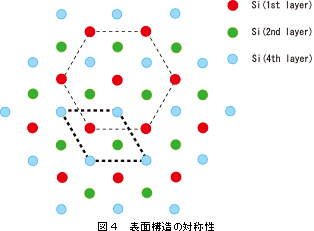
今回の半導体表面での発見は、電子スピンの垂直起立が実現する条件として、表面構造の対称性により理論的に特定された点でも重要です。この対称性を満たす表面構造あるいは界面構造であれば、一般的に電子スピンの垂直起立が観測されるということです。したがって、今後の表面構造の設計指針を示しているということになります。対称性の条件の解明には、理論的な手法である第一原理計算と群論が大いにその役割を果たしました。具体的に対称性について述べて行きましょう。
今回問題にしている表面は、図４のような原子配列と同じ対称性（規則性）をもっています。実際に実験で使用した系は、表面を上から見たときに緑色位置にタリウム（元素記号Ｔｌ、原子番号８１）が配置されています。例えば赤い原子を中心にみて、120度回転させた構造はやはり元の構造と同じです。もちろんその反対向きに120度回転させた構造についても元の構造に戻ります。次に鏡映操作を考えます。鏡のように左右対称な対称性です。最も近接する赤色同士を結んだ直線の右側と左側では、緑が青に青が緑に移りもとの構造へは戻りません。しかし次に近くにある（次近接の）赤色同士を結んだ直線の右側と左側では左右対称になっています。このように見てくると、図には120回転とその逆回転の２つの回転対称性と３つの鏡映対称性が存在します。図４にはそれらの他にも別の種類の対称性があります。それは冒頭でお話した並進対称性です。青色を結んだ平行四辺形をみてください。この部分は、ある２方向へ平行移動することによりもとの構造へ重なることが分かります。これが２次元結晶の対称性です。このような対称性のすべてが、上記の電子の方程式中で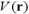
に含まれています。群論という数学的理論を用いることにより、対称性から波動関数である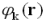および固有値である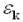の性質を知ることができます。完全に性質を知るためには方程式を解く以外にはありませんが、群論により一般的な性質を知ることができるため、細かな数値解析結果を見るよりも全体の性質を正確に把握することが可能です。今回、群論により電子スピンが垂直起立することが数学的にも明らかになりましたし、あらかじめ計算していた第一原理計算の結果とも一致するものでした。対称性についてまとめると、図４のような表面構造にある電子では、最近接の赤色を結んだ方向に、電子がある波数の大きさで運動するときに、電子スピンが垂直起立することが分かったのです。