第一原理計算とは、計算対象となる物質系を構成する元素の原子番号と系の構造を入力パラメータとし、実験結果を参照しないで系の電子状態を求める最新の計算手法である。
【第一原理電子状態計算】
身の回りの物質、生命をもつ物質、あるいは電子デバイスを構成する物質等は、原子核と電子から構成されている。このような系は、質量が大きく異なる粒子が混在する系である。原子核の質量は、電子の質量に比較して非常に大きい。電子の質量は、最も単純な水素原子の原子核である陽子の質量の1836分の1程度であり, 例えば, 炭素原子の質量は電子質量の約22000倍である。多くの原子核は、量子性（粒子性と波動性をもつ物質の性質）が小さく、古典的運動方程式（ニュートンの運動方程式）に従い、電子の運動については、量子性が欠かせない。電子は、その質量、電荷の他に, 角運動量の固有な量を持っている。これはスピン角運動量と呼ばれる。電子の運動は、電子の波動関数を求めることにより解析される。方程式は、ディラック方程式やシュレディンガー方程式である：
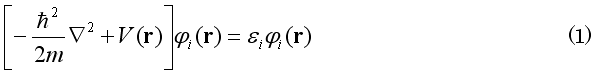
[ ]内は、ハミルトニアンと呼び、運動エネルギーとポテンシャルエネルギー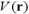
の和である。ポテンシャルエネルギーは、原子核からの引力と他の電子からの斥力である。この方程式ではハミルトニアンを与え、波動関数
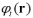と固有値
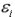を求める。ハミルトニアンを演算子とみると、この演算子の固有値と固有状態を求める固有値問題である。波動関数の絶対値の２乗
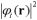が電子密度の空間分布を表している。このように量子状態
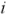の波動関数と固有値を求めることにより電子の状態が解析される。２成分の波動関数を採用することにより量子状態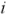のスピン状態も解析することができる。
原子核からのポテンシャルは、原子核の元素の種類とその位置を指定することにより決定することができる。他の電子からのポテンシャルを含んだ全ポテンシャルを極力現実的に計算する計算方法を第一原理計算と呼んでいる。他の電子からポテンシャルを電子密度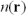
の関数として与える方法を密度汎関数法と呼んでいる。この密度汎関数法の開発を評価されて、1998年にW. Kohnはノーベル賞を受賞した。シュレディンガー方程式などから波動関数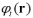が求まったら、次に電子密度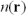を計算する：
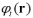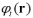この電子密度からポテンシャルを計算し、再度式(1)からを計算し、や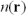が変化しなくなるまでこのような計算を繰り返し、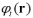や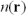を決定する。このようなものを自己無撞着な計算法（セルフコンシステント計算法）と呼んでいる。
固体内や固体表面に対して計算した固有値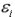を電子の量子数である波数ベクトル
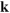の関数として得られるものが、電子バンドである。これは電子状態の重要な物理量であり、これを観測する強力な方法として角度分解光電子分光やスピン偏極角度分解光電子分光がある。後者は、物質中の電子のスピン角運動量状態を測定する有力な方法の一つである。