コンピュータで探る相転移
コンピュータで探る相転移その１
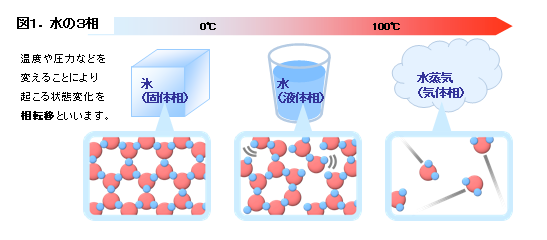
常圧下の水は０℃以下では氷、１００℃以上では水蒸気になります(図1)。氷(固体相)から水(液体相)への変化のように、温度や圧力などを変えることで起こる巨視的な状態変化を相転移といいます。
相転移現象を数学・物理学に基づいて数式だけを用いて説明することには限界があります。そこでコンピュータを用いることにより相転移のような複雑な現象に直接アプローチすることが重要となっています。
最初のコンピュータ(ENIAC)は1946年に発明され、いち早くアルダーらは剛体球モデルを用いたコンピュータシミュレーションにより固体―液体相転移を調べました。剛体球モデルは原子・分子間に引力がない斥力だけの単純なモデルですが、物質の結晶化が斥力のみで起こることを理論的に示した重要なシミュレーションとして知られています。
コンピュータで探る相転移その２
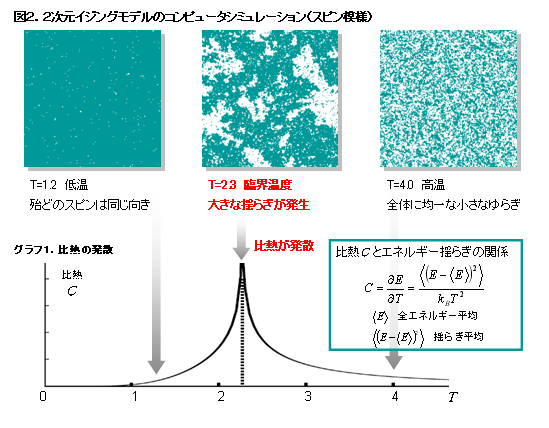
イジング模型は強磁性体(磁石)の性質、秩序―無秩序相転移、２次相転移などを探る統計力学のモデルとして使われています。格子点上には上向き↑または下向き↓のスピンがあり、隣同士とだけ相互作用します。
隣同士のスピンが同じ向きであればエネルギーが低くなり、反対向きであればエネルギーが高くなることを示しています。物理法則によればスピンの向きは全エネルギーが低くなるように向きを揃えようとします。それと同時に、温度による乱雑さを増大させる効果(エントロピー)のために反対向きのスピンも発生します。競合する２つの効果のために、秩序相(低温)と無秩序相(高温)が存在することになります。この間の相転移現象はコンピュータを用いて日本で実施された重要なシミュレーションの一つです。
物質中電子のシミュレーション：磁性編
スピン軌道相互作用
原子核の周りを軌道運動する電子は、２種類の角運動量を持っている。
\(
\begin{equation*}
\left\{
\begin{array}{1}
\bf{軌道角運動量} & \vec{l} \\
\bf{スピン(自転)角運動量} & \vec{s}
\end{array}
\right.
\end{equation*}
\)
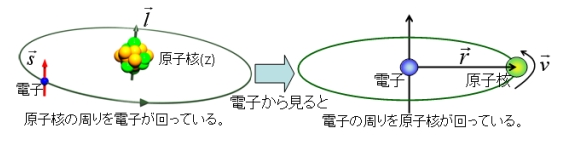
原子核の運動が作る軌道電流\((-\vec{v})Ze\)による有効磁場は、(ビオ・サバールの法則により)電子の位置で、
\(
\begin{equation*}
\displaystyle{\vec{H}=\frac{Z|e|}{c}\frac{(\vec{r}\times \vec{v})}{r^3}=\frac{Z|e|(\vec{r}\times m\vec{v})}{mcr^3}=\frac{Z|e|}{mcr^3}\vec{l}}
\end{equation*}
\)
である。この磁場とスピン磁気モーメントの相互作用エネルギーは、
\(
\begin{equation*}
\displaystyle{H_{SO}=-\vec{\mu}_s\cdot\vec{H}=\frac{Ze^2}{m^2c^2r^3}\vec{l}\cdot\vec{s}}
\end{equation*}
\)
となる。電子が静止していると考えたが、実際には電子が軌道運動しているため、相対論的補正が必要であり、因子1/2が付く。結果スピン軌道相互作用は、
\(
\begin{equation*}
\displaystyle{H_{SO}=\frac{Ze^2}{2m^2c^2r^3}\vec{l}\cdot\vec{s}}
\end{equation*}
\)
と書くことができる。
スピン軌道相互作用は、スピン磁気モーメントと軌道磁気モーメントを平行、または反平行に揃えようとする。
スピン軌道相互作用は相対論的効果であり、ディラック方程式(相対論的電子論)から自然に導かれる。
\begin{equation*}
\left.
\begin{array}{1}
\bf{電子の遠心力 = 原子核の静電引力} & \displaystyle{m\frac{v^2}{r}} = \displaystyle{\frac{Ze^2}{r^2}} \\
\bf{ボーアの量子化条件} & mvr = n\hbar
\end{array}
\right\}
\displaystyle{\frac{v}{c}=\frac{Z}{137}\frac{1}{n}}
\end{equation*}
\)
金(Z(Au)=79)では、\(n=1\)のとき\(\displaystyle{\frac{v}{c}\approx 0.58}\) (相対論的効果が無視できない)
原子番号の大きな原子を含む物質の物性をあつかうときには、スピン軌道相互作用などの相対論的効果を考慮した計算を行う必要がある。
スピン軌道相互作用に起因する物性の例
磁気異方性
スピン軌道相互作用があるとスピンの回転に伴い、軌道の波動関数の重なりの変化が生じるため、結晶の磁化方向により内部エネルギーの変化が生じる。
これにより、磁化しやすい方向(磁化容易軸方向)と磁化しにくい方向(磁化困難軸方向)が現れる。また、磁化方向に依存する内部エネルギーを磁気異方性エネルギーと呼ぶ。
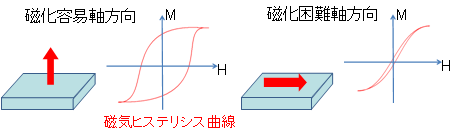
クリップ磁石では、面直方向が容易軸方向となっているため磁極が面直方向にできている。また、磁石の保持力は磁気異方性エネルギーが大きいほど大きくなる。
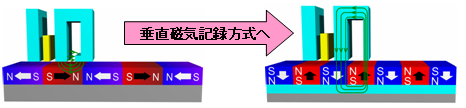
ハードディスクの記録密度の向上に向けて、垂直磁気記録方式の磁気記録メディアの開発が盛んである。より記録密度の高い垂直磁気記録メディアの磁性材料には、容易軸が面直で、熱により磁化の方向がバラバラになるのを防ぐために磁気異方性エネルギー(保持力)の大きな材料が求められる。
ラシュバ効果
次世代デバイスの１つであるスピン電界効果トランジスタ(図1)では、ゲート電界でスピン軌道相互作用を制御することにより、スピンを操作する。
スピン軌道相互作用は以下のように書き換えることができる。
\(
\begin{equation*}
\displaystyle{H_{SO}=-\frac{1}{2m^2c^2}(\vec{E}\times\vec{p})\cdot\vec{s}}
\end{equation*}
\)
ゲート電界\(\vec{E}\)を変えることで、スピンに働く有効的な磁場\(\vec{H}_{eff}(=\vec{E}\times\vec{p})\)を制御することができる。
電子から見ると図2のように、電流\(\vec{I}\)が流れており、この電流が電子の位置に磁場を作る。この磁場を軸としてスピンは歳差運動を行う。
表面や界面では、\(\nabla V \parallel z\)で、
\(\displaystyle{H_{SO}=\frac{\hbar^2}{4m^2c^2}(\nabla V)_z(k_x\sigma_y-k_y\sigma_x)} \)
(ラシュバのスピン軌道相互作用)
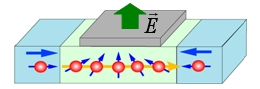
図1 スピン電界効果トランジスタ
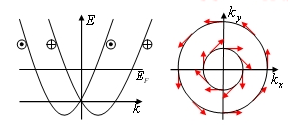
図3 ラシュバスピン軌道相互作用によるバンドの分裂
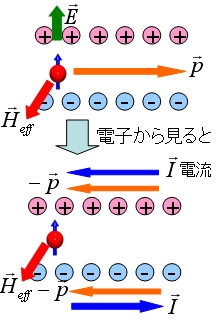
図2 スピン軌道相互作用による電子の運動
液体酸素のシュミレーション
酸素は、大気の約5分の1を占め、人間などの生命活動に欠かせない重要な物質である。名前がよく知られているにも関わらず酸素分子が分子磁石であることは意外に知られていない。
酸素分子は、酸素原子が2つ結合した分子で通常の状態では、分子単位で電子2個分に相当する磁気を持っている(図1参照)。この特徴は、酸素の特異な性質を作り出す一因となっていると考えられる。酸素分子の磁気の方向を揃えて配置することが可能ならば、マクロな磁石をつくることも可能となるが、現在のところ常圧以外の条件でもそのようなものは見出されていない。酸素は、常圧では-183.0℃(絶対温度90.2K)で液化し、-218.4℃(54.8K)で固相に相転移する。固相は高温側から\(\gamma\)相、\(\beta\)相、\(\alpha\)相の異なった分子配列をもつ3相が存在する。
液体酸素は、涼しげな淡青色をしている液体である。空気を液化すると青みがかった液体になるのは、このためである。この液体は赤色の光を吸収しているので、その補色である青色がみえるのである。2つの酸素分子が力をおよぼしあう程度に近接したときにちょうど赤色の光が入ってくると光は吸収されると考えられている。
2つの酸素分子は、お互いの磁気を打ち消すように近接する。この特徴はシミュレーションの結果からも顕著である(図2参照)。赤く色を付けた分子は、互いに近接している分子を示したもので、そのときの磁気の方向に注意してシミュレーションの結果を観察してほしい。矢印の向きが反対向きになっているのが分かると思う。このとき、2つの会合する分子は、多くの場合、長方形の形を作っている。
このように液体酸素では、磁気と分子配置が密接に関係していることがわかる。単なるフェライト磁石から、上記のような酸素分子を始め地球規模では地磁気、人体中では例えば液体中のヘモグロビン、工業製品では磁気記憶素子、磁気半導体デバイスなど、生活の様々な場面や生命活動の種々のプロセスで磁気は、重要な役割を担っている。磁性体のシミュレーションプログラムの幅広い応用が大いに期待される。
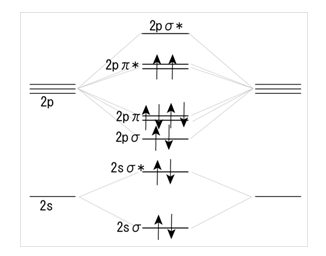
図1 酸素分子の電子構造
この図は少々専門的な記述法で描かれている。電子は本来上向きスピンと下向きスピンと呼んでいる個性をもっている。通常上向きスピンと下向きスピンはペアとなっていることが多いが磁気を示す物質中では図のように完全にペアを組まずにスピンが同じ向きを向く場合\((2\rm{p}\pi*)\)が存在している。典型的な磁性物質である鉄の場合原子あたり平均電子2.2個分に相当する磁気をもっている。
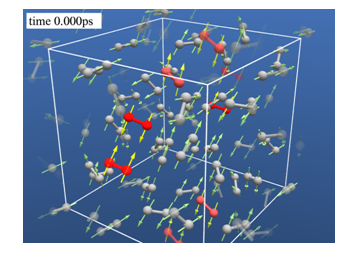
図2 液体酸素の分子配置と磁気配置
ダンベルの形をしたものが分子を表しており、矢印が磁気の方向を示している。分子間距離が3.2Å以内になった分子の色を赤く色付けしている。濃い赤は、3.0Å以内の分子の組を示している。赤色ペアの磁気は、上向きスピンと下向きスピンがペアを作っているのが分かる。ペアを作るとき2つの分子は多くの場合長方形構造を作っている。白い線は、シミュレーションの箱を示している。箱の外に出て行った分子は反対側から箱の中に入ってくるようになっている。箱の外に出たときに突然分子が消えるのではなく徐々に消えるように表現が工夫されている。ps(ピコ秒)は\(10^{-12}\)秒である。
超高圧下でのシュミレーション
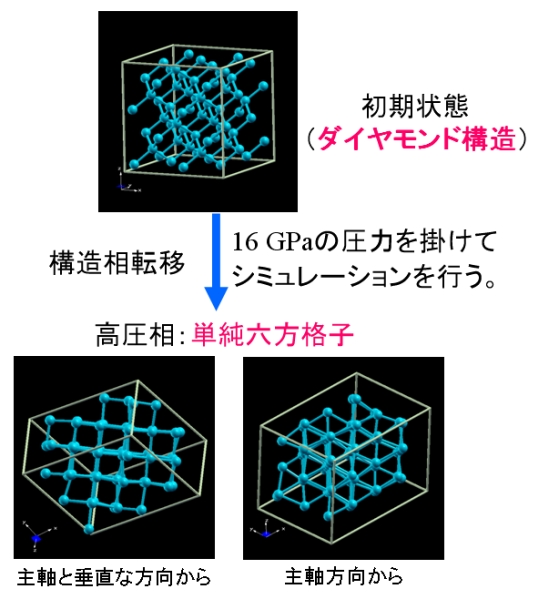
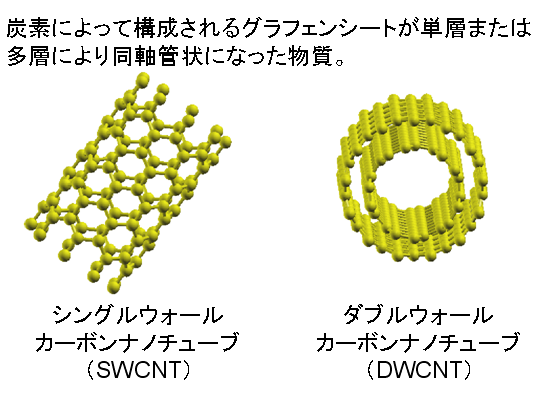
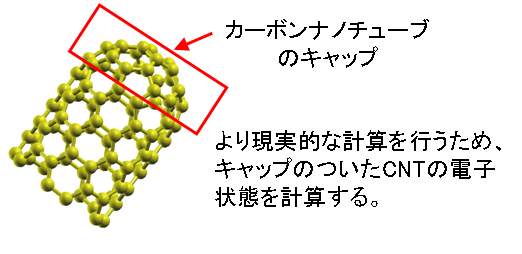
カーボンナノチューブ(CNT)
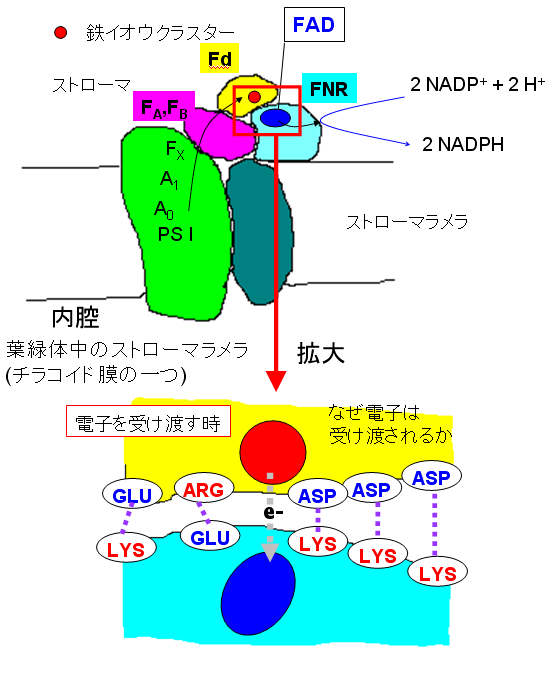
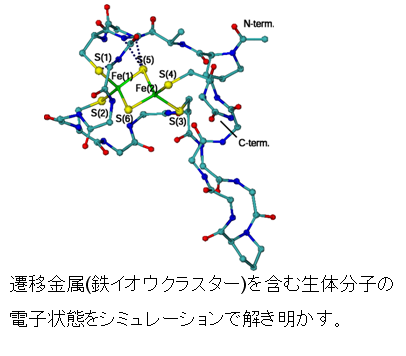
フェレドキシンタンパク質
